1up noob: 2018

2018/07/25

【Windows10】SSD(120GB)からSSD(500GB)にクローンして換装した

今年のPrime DayでCrucialのMX500を購入しました。

現在使用しているデスクトップPC（7年選手）のSSDの容量が120GBと少なく、容量がほぼ限界まできていたので、SSDを比較的大容量のものに入れ替えることにしました。
これまで、グラフィックボードや電源の交換の経験はありますが、ストレージの入れ替えはノートパソコンのHDDぶりです。
ド素人なりに、忘備録を残しておきます。

新しいSSD

元のSSD

データ移行のため、SSD接続用にAUKEYの2.5インチSSD ケースを使いました。

SSDのクローン作業はすぐ終わると思っていましたが、予想外に手間取り結局何度か試すことになりました。
元よりも容量が大きいSSDへの移行だったため、パーティションサイズを変更してクローンしたかったのですが、うまく扱えませんでした。最終的に、おすすめ記事が多いEaseUS Todo Backup Freeではなく、AOMEI Backupper Standardを使いました。

クローン後は、元のSSDが繋がっていたSATAに差し替えて換装完了です。
問題なくWindowsも起動しました。

換装前後のCrystalDiskMarkのベンチマークスコアは以下の通りです。


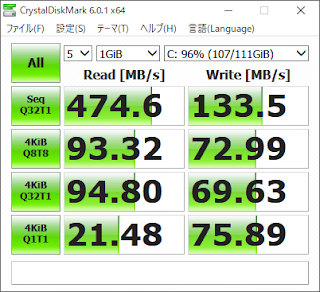A-DATA S511(120GB)	Crucial MX500(500GB)

容量にかなり余裕ができ、書き込み速度も向上し、大変満足のいく結果となりました。

2018/06/10

【R】ネットワーク分析(igraph)でハブ空港を見つける

igraphは、グラフの可視化や中心性解析などが出来るRのパッケージです。
OpenFlights.orgのデータを使って、世界の空港のネットワークグラフを作成し、igraphを用いて、ハブになる空港を表示してみました。

【実行環境】
macOS 10.13.5
R version 3.4.4

まず、はじめにOpenFlights.orgのデータのairports.datとroutes.datをExcelなどで編集し、Pajek形式にまとめました。このネットワークは、各空港(ノード)とそれぞれを結ぶ直行便(エッジ)で構成されています。

直行便がより多い空港がより重要なハブ空港であると仮定して、page.rank関数を用いてページランクを計算しました。

library(igraph)
g <- read.graph("airports_link.net", format="pajek")
score <- page.rank(g, weights = NA)$vector
sort(score, decreasing=T)[1:10]

上位10位の計算結果は、以下のようになりました。(空港名でなく、空港がある都市名になっています。)
1. Atlanta
2. Chicago
3. Los Angeles
4. Dallas-Fort Worth
5. Paris
6. London
7. Singapore
8. Beijing
9. Denver
10. Frankfurt

雑ですが、可視化も行ってみました。

xy <- cbind(V(g)$y, V(g)$x)
V(g)$size <- 1
V(g)$frame.width <- 0.1
E(g)$width <- 0.02
E(g)$color <- "green"
E(g)$arrow.size <- 0.02
plot(g, layout=xy)

全体的に雑な分析になってしましましたが、Rはパッケージも充実しており可視化も容易なので、今後も使って行こうと思います。

2018/01/08

【Python】バリオグラムを計算する

地球統計学での内挿法の一つであるクリギング法では、データが距離と方向にどのような関係を持つかを表すバリオグラムを元に重み付けを行います。バリオグラムやクリギング法については下記の書籍を参考に、バリオグラムを計算するプログラムをPythonで書きました。

x,y,valueという並び順のcsvで与えたデータに対して、バリオグラム（等方性）を計算します。
バリオグラムを計算したのち、指定した理論バリオグラムの形にフィットする値を計算します。

実行環境

Python 3.6.1

デモファイルに対する実行結果

【関連記事】